MIT’s New FSNet Tool Solves Complex Power Grid Challenges in Minutes With Guaranteed Feasibility

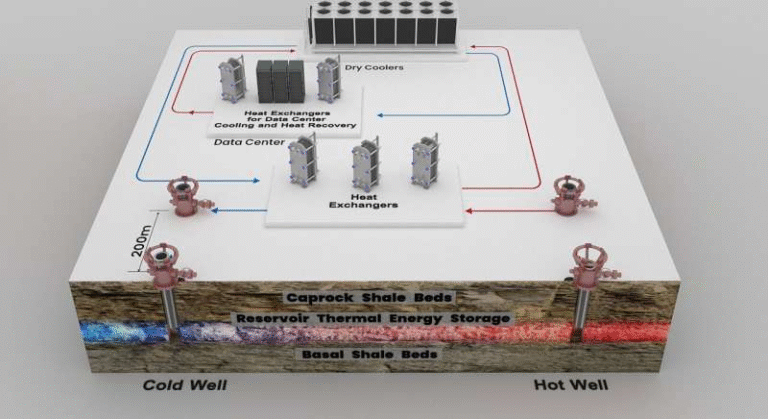
Managing a modern power grid has become one of the most difficult optimization tasks in engineering. Operators constantly need to figure out how much power should be produced, where it should flow, and how to do all of this while keeping costs low and avoiding overloads on infrastructure. These decisions have to be recalculated again and again as demand and renewable generation fluctuate from moment to moment. Traditional optimization tools can deliver mathematically optimal results, but they often take far too long when the system is large and constantly evolving. On the other side, machine-learning models are incredibly fast but tend to violate important system constraints, making their solutions unusable in practice.
Researchers at MIT have developed a new approach called FSNet that aims to combine the best of both worlds—the speed of machine learning and the reliability of classical optimization. FSNet is designed to find feasible, high-quality solutions to complicated power grid problems in a fraction of the time traditional solvers need. Instead of letting a neural network directly generate a final solution, FSNet introduces a careful refinement step that ensures no system limits are violated.
Below is a clear and detailed breakdown of how FSNet works, why it matters, and what additional insights it brings to the broader field of constrained optimization.
What Problem FSNet Is Trying to Solve
Power grid operators face a constant stream of optimization tasks, such as determining how much electricity each generator should produce, or how to direct the flow of power across transmission lines. Each of these tasks comes with a large set of equality and inequality constraints—for example:
- Power output must match demand
- Voltage levels must stay within specific ranges
- Transmission lines must not exceed safe capacity
- Generators cannot exceed their physical limits
Traditional solvers treat these constraints with mathematical rigor and guarantee feasible solutions, but as systems grow and become more dynamic, solving these problems can take hours or even days. This delay is unacceptable when grid conditions are changing rapidly.
Machine-learning models, meanwhile, can guess solutions almost instantly by learning from past data. But because of small training errors or mis-representations of the problem, they often generate answers that break important system rules—something operators simply cannot risk.
FSNet specifically targets this gap: finding solutions that are fast to compute, yet guaranteed to be feasible.
How FSNet Actually Works
FSNet uses a two-step method that blends neural networks with an embedded optimization loop:
- Neural Network Prediction
A neural network quickly predicts an approximate solution to the optimization problem. This step captures patterns and structures in the data that traditional solvers do not exploit. - Feasibility-Seeking Refinement
Instead of stopping at the prediction, FSNet runs a built-in optimization routine that repeatedly adjusts the neural network’s output.
This refinement step ensures the final answer satisfies every constraint. It targets both equality and inequality constraints simultaneously, which makes the method flexible and easier to apply across different kinds of problems.
The key idea is that the neural network is not responsible for perfection—it only needs to provide a starting point close enough for the refinement step to finish the job effectively.
This two-step design helps FSNet avoid the biggest issue with pure machine learning: lack of constraint satisfaction. At the same time, it avoids the slow solve times of classical optimization by starting with a good estimate rather than searching blindly.
Performance Compared to Traditional Tools
Researchers tested FSNet on a wide range of challenging optimization tasks, including power grid problems. Across these experiments, FSNet consistently:
- Worked several times faster than traditional solvers
- Delivered solutions that never violated constraints
- Outperformed pure machine-learning methods, which often failed to meet grid requirements
- Even found better solutions than traditional solvers in extremely complex cases
The last point surprised the researchers. It suggests that FSNet’s neural network component can learn hidden patterns in the training data—patterns that allow it to identify feasible regions of the problem space that classical solvers may not discover as efficiently.
This combination of speed and reliability makes FSNet particularly attractive for domains where decisions need to be recalculated constantly in real time.
Why This Matters for Power Grids
Modern power grids are becoming more difficult to manage due to two major trends:
- Rising renewable energy use, which increases variability
- More distributed energy resources, such as rooftop solar and small-scale storage systems
These changes mean the grid must respond more quickly to shifts in supply and demand. Operators increasingly need optimization tools that can compute feasible answers in minutes or even seconds, not hours.
Because FSNet guarantees feasibility, its solutions can be trusted in real-world power systems where safety and reliability are critical. And because it is so much faster than traditional solvers, it could enable operators to update decisions more frequently, improving resilience and efficiency.
Broader Uses Beyond Power Grids
While FSNet was tested on grid-related tasks, its design is general enough to apply to any optimization problem with constraints. Potential applications include:
- Product design: ensuring physical or performance requirements are met
- Supply chain planning: optimizing production schedules with resource limits
- Financial portfolio management: meeting risk or allocation constraints
- Manufacturing and logistics: improving throughput without violating operational constraints
Any system that relies on constrained optimization, especially in environments where calculations must be fast and reliable, could benefit from FSNet.
Limitations and Future Improvements
Despite its strengths, FSNet has a few areas the researchers plan to improve:
- It currently requires more memory than ideal, especially when scaling up to massive real-world problems.
- The researchers want to integrate more efficient optimization algorithms to increase performance.
- Scaling FSNet to extremely large and highly realistic problems remains a challenge that they aim to tackle over time.
Still, as an early-stage approach, FSNet is already demonstrating strong potential.
Additional Background: Why Feasibility Matters in Optimization
Constraints are fundamental in physical systems. Breaking them—even slightly—can lead to catastrophic failures. For example:
- Overloading a power line can cause outages
- Violating voltage limits can damage equipment
- Exceeding generator capacity can trigger safety shutdowns
This is why researchers emphasize guaranteed constraint satisfaction. A fast solution is useless if it breaks real-world limitations. FSNet’s main contribution is making machine learning more trustworthy for these kinds of tasks by giving explicit control over feasibility.
Additional Background: How Neural Networks Help in Optimization
Neural networks excel at recognizing patterns and approximating functions. In optimization, this can be useful because:
- Many systems exhibit repeating patterns over time
- Real problems may follow certain structures that classical solvers cannot exploit
- Neural networks can drastically reduce the number of calculations needed
FSNet’s hybrid approach leverages these strengths without sacrificing the rigor needed in engineering applications.
Research Reference
FSNet: Feasibility-Seeking Neural Network for Constrained Optimization with Guarantees
https://arxiv.org/abs/2506.00362