Duke University Researchers Develop an AI That Can Discover Simple Equations Behind Complex Systems

Researchers at Duke University have introduced a new artificial intelligence framework that tackles one of the hardest problems in science: understanding extremely complex systems using simple, human-readable equations. The work shows how AI can move beyond pattern recognition and into the realm of scientific reasoning, helping researchers uncover the hidden rules that govern systems ranging from swinging pendulums to global climate patterns.

The study was published in the journal npj Complexity and presents a method that allows AI to analyze experimental data from dynamic systems and automatically generate compact mathematical descriptions that remain accurate over long periods of time.

How Scientists Traditionally Understand Complex Systems

Many systems in nature and technology are governed by countless interacting variables. Weather systems, electrical circuits, mechanical devices, and biological networks all evolve over time in ways that can appear chaotic and unpredictable. Historically, scientists have relied on simplified equations to make sense of this complexity.

Classic examples include Newton’s laws of motion, which reduce the behavior of moving objects to a small set of variables such as force, mass, and acceleration. Even though real-world motion involves air resistance, temperature, surface texture, and other influences, simple equations often capture the essence of the behavior remarkably well.

However, finding these simplified equations becomes nearly impossible when systems involve hundreds or thousands of variables, especially when the underlying physics is unknown or too complicated to express mathematically.

What This New AI Framework Does Differently

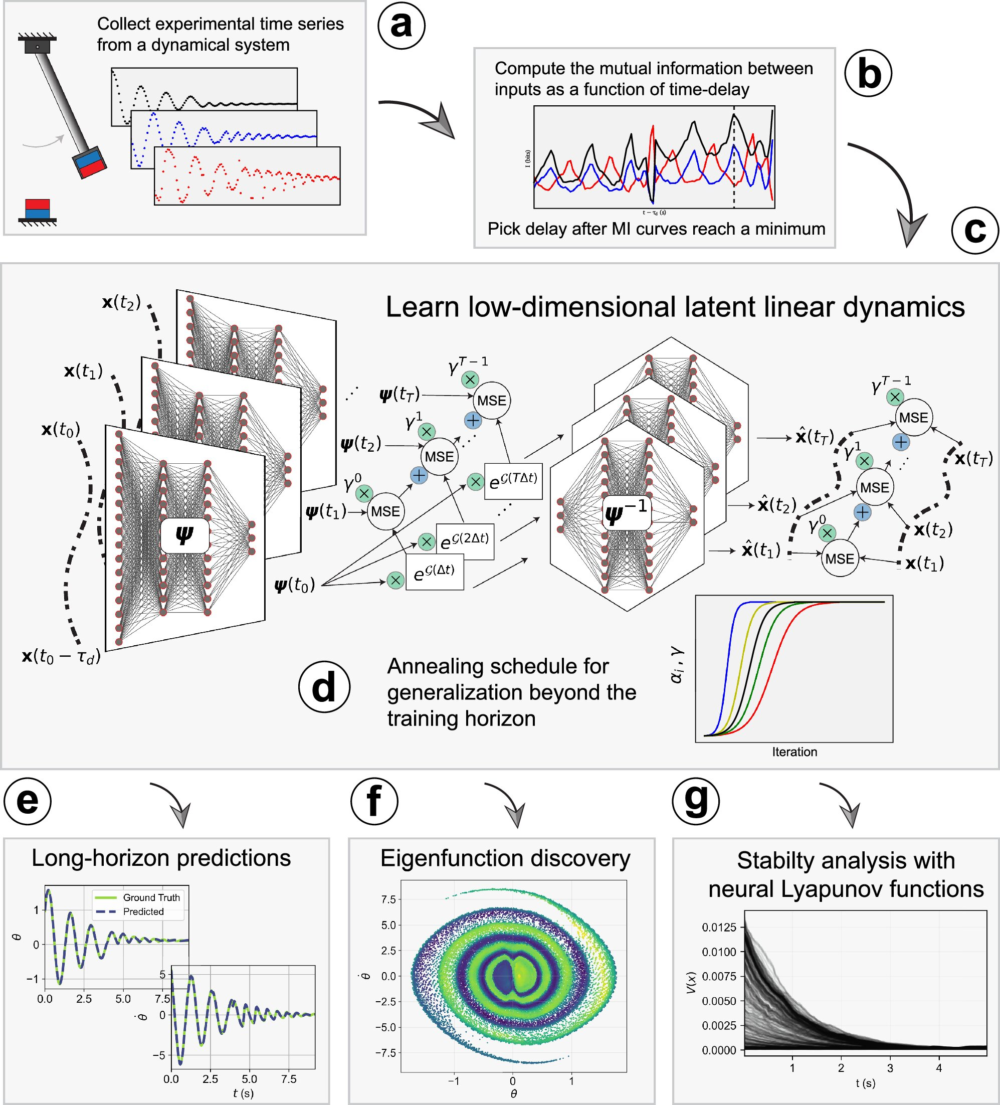
The Duke research team developed an AI system that mimics the way early physicists discovered fundamental laws, but at a scale that far exceeds human cognitive limits. Instead of starting with known equations, the AI begins with raw time-series data—measurements showing how a system evolves over time.

Using this data, the AI identifies patterns in the system’s evolution and constructs a low-dimensional representation that captures its essential dynamics. In simple terms, the system finds a small set of hidden variables that explain how the entire system behaves.

What makes this approach especially powerful is that the final output behaves mathematically like a linear system, even when the original system is highly nonlinear and chaotic. Linear systems are much easier for scientists to analyze, predict, and interpret.

Inspired by a Nearly Century-Old Mathematical Idea

The framework builds on a concept introduced in the 1930s by mathematician Bernard Koopman, who proposed that nonlinear systems could be described using linear operators if viewed in the right mathematical space. While the idea was theoretically elegant, it was impractical for complex systems because it required an overwhelming number of equations and variables.

This is where AI makes the difference. The Duke team’s method uses deep learning combined with physics-inspired constraints to automatically discover the right coordinate system where the dynamics become linear—without needing thousands of equations.

In many cases, the AI reduced systems to models that were more than ten times smaller than those produced by earlier machine-learning approaches, while still maintaining accuracy over long-term predictions.

Tested on a Wide Range of Systems

To demonstrate its versatility, the researchers applied the framework to many different types of systems:

• Mechanical systems, including simple pendulums and chaotic double pendulums
• Magnetic pendulums, where magnets introduce nonlinear interactions
• Electrical circuits with complex oscillatory behavior
• Climate models, such as temperature variations across the globe over time
• Neural circuit models, which capture rhythmic biological activity

Despite the vast differences between these systems, the AI consistently identified small sets of governing variables that dictated their behavior. This suggests the framework is not limited to one field but can serve as a general tool for studying dynamical systems.

Understanding Stability and Long-Term Behavior

Beyond prediction, the AI framework can identify attractors, which are stable states toward which systems naturally evolve. These stable states are crucial for understanding whether a system is behaving normally, drifting toward instability, or undergoing a fundamental transition.

For scientists who study dynamical systems, finding these structures is like identifying landmarks on a map. Once the attractors and stable regions are known, the system’s overall behavior becomes much easier to interpret.

This capability is especially valuable in real-world applications where instability can have serious consequences, such as power grids, climate systems, or biological rhythms.

Why Interpretability Matters

One of the standout features of this research is interpretability. Many modern AI models are powerful but opaque, offering accurate predictions without explanations. In contrast, this framework produces compact linear equations that scientists can directly analyze and connect to existing theories.

Because the resulting models align with traditional mathematical tools, researchers can use decades—or even centuries—of established methods to explore them further. This bridges the gap between AI-driven discovery and human scientific understanding.

The goal is not to replace physics or mathematics, but to extend scientific reasoning into domains where traditional equations are missing, incomplete, or too complex to derive manually.

When Traditional Physics Falls Short

In many experimental settings, researchers do not know the governing equations in advance. This is common in biological systems, complex materials, and emerging technologies. Writing down exact equations may be impractical or impossible.

The new AI framework excels in these situations by learning directly from data and producing models that are both accurate and interpretable. This makes it especially useful for exploratory science, where the goal is not just prediction but understanding.

Future Directions for the Research

The Duke team sees this work as part of a broader effort to develop “machine scientists”—AI systems that actively assist in scientific discovery. Future plans include using the framework to guide experimental design, helping researchers decide what data to collect in order to reveal a system’s structure more efficiently.

They also aim to extend the approach to richer data types, including video, audio, and complex biological signals, where dynamics are often hidden in high-dimensional measurements.

As AI continues to evolve, this research points toward a future where machines do more than process data—they help uncover the fundamental rules that govern the physical and living world.

Additional Context: Why Linear Models Are So Valuable

Linear models are a cornerstone of science and engineering because they are mathematically tractable. They allow researchers to predict behavior, analyze stability, and understand cause-and-effect relationships with relative ease.

Transforming nonlinear systems into linear ones—without losing essential behavior—is often considered a holy grail in dynamical systems research. This new AI framework shows that such transformations are not only possible but can be automated and generalized across disciplines.

Research Paper Reference

Automated Global Analysis of Experimental Dynamics Through Low-Dimensional Linear Embeddings
https://www.nature.com/articles/s44260-025-00062-y