Zero Lasing Modes in Topological Lasers Are Not Always Topological, New Physics Study Shows

The world of topological photonics has been buzzing for years, especially with the promise of building lasers that are naturally robust against defects, disorder, and fabrication errors. At the heart of this idea is a simple assumption: if a photonic structure hosts a topological zero mode, then that mode should dominate laser emission when gain is applied. A new study, however, shows that reality is more subtle. According to fresh research published in Communications Physics, zero lasing modes do not always retain their topological nature, even when the underlying structure is topological.

This finding adds an important layer of nuance to how scientists think about topological lasers, particularly when nonlinear effects like gain saturation are taken seriously.

The basic idea behind topological lasers

Topological lasers are built on concepts borrowed from condensed matter physics. In simple terms, topology deals with global properties of a system that remain unchanged even when the system is distorted. In photonics, this has led to structures where light can travel or localize in very specific ways that are protected against imperfections.

A common recipe for creating a topological laser involves three steps. First, researchers design a cavity or waveguide array that supports topological modes, often localized at the edges of the system. Second, they apply optical pumping in a way that favors these edge or surface states. Finally, they ensure the system reaches a stable lasing state. Many experiments using photonic topological insulators and Su–Schrieffer–Heeger (SSH) lattices have successfully demonstrated lasers operating in such protected modes.

For a long time, this approach seemed solid. But most demonstrations either ignored nonlinear effects entirely or treated them as a secondary issue.

Why nonlinear effects matter in real lasers

Real lasers are inherently nonlinear systems. As light intensity increases, the optical gain provided by the medium does not grow indefinitely. Instead, it saturates. This phenomenon, known as gain saturation, can significantly reshape how light distributes itself across a laser array.

Earlier theoretical studies often focused on whether a topological laser mode is stable or unstable once lasing begins. The new study takes a different route. Rather than emphasizing instability, the authors specifically look at regimes where the zero mode is the only stable lasing solution. This makes the results especially relevant for practical devices, where engineers aim for clean, single-mode operation.

What the new study actually shows

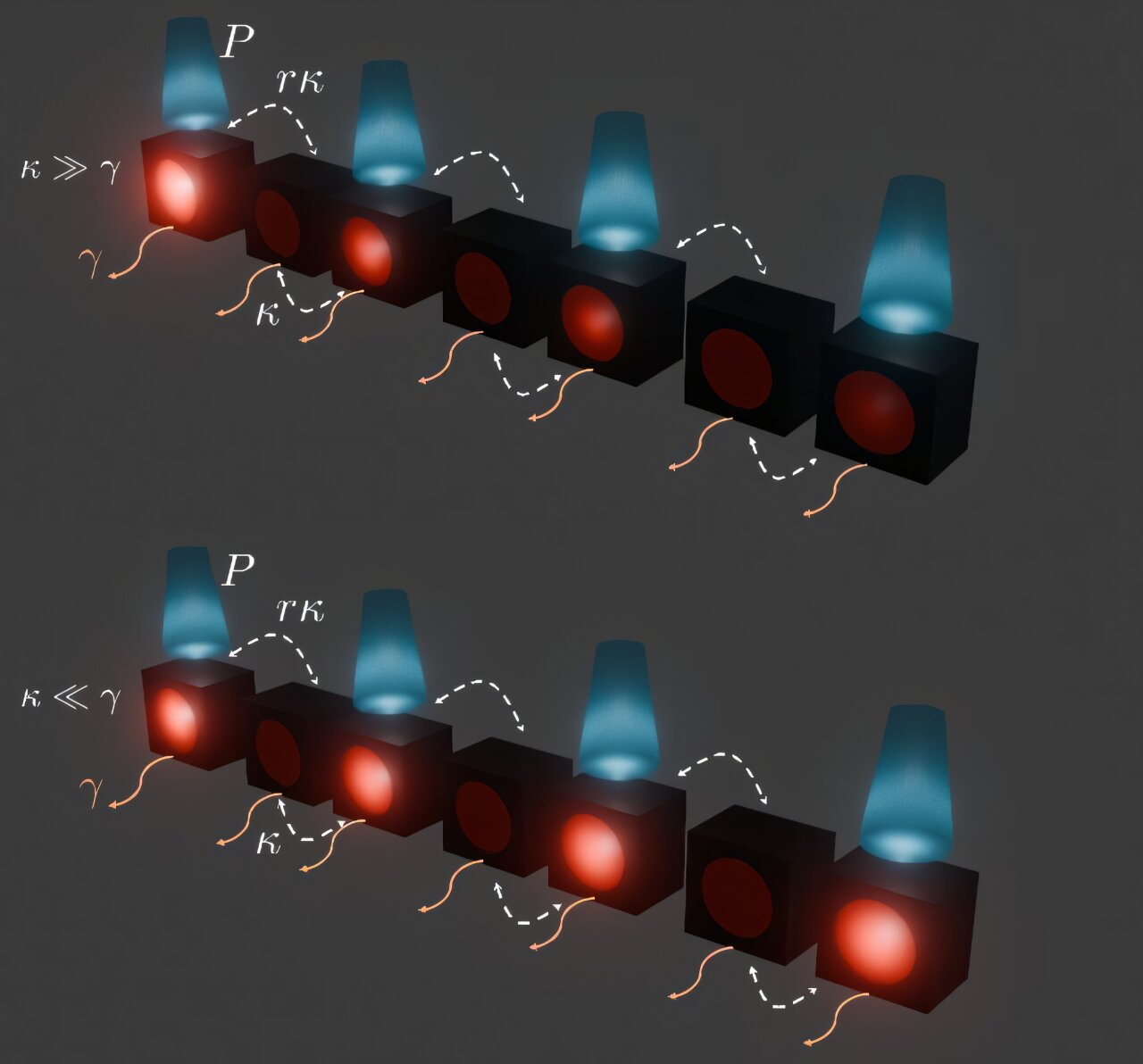
The research focuses on an SSH lattice, a well-known one-dimensional model that supports a topological zero-energy edge state when the couplings between sites alternate in strength. In the passive, linear version of this lattice, the zero mode is strongly localized at the edge.

The researchers explored what happens when this system is turned into a laser by adding gain and loss, making it a non-Hermitian system, and by including nonlinear gain saturation. Crucially, they examined how the lasing mode behaves as the overall coupling strength between lattice sites is varied, while keeping the ratio between strong and weak couplings fixed.

In the regime of strong coupling, the lasing zero mode closely resembles the expected topological edge state. It remains localized and behaves much like the zero mode of the underlying passive lattice.

However, the situation changes dramatically when the coupling becomes weak. In this limit, the study finds that the lasing zero mode can become delocalized, spreading its intensity almost uniformly across the entire array. Even though the lattice itself is still topological, the lasing mode no longer reflects that topology in its spatial profile.

This is a key result: a lasing zero mode does not automatically imply a topological edge state.

The physical intuition behind the result

The reasoning behind this behavior is surprisingly intuitive. If all couplings between sites are gradually reduced toward zero, while the system is uniformly pumped, each site effectively behaves like an independent laser. Under equal pump conditions, these sites should emit similar amounts of light.

Introducing very small couplings does not immediately destroy this uniform distribution. As a result, there exists a regime where the lasing mode naturally favors a nearly flat intensity profile, even though the linear, passive system would support a localized edge mode.

The balance between inter-site coupling and optical loss, combined with nonlinear gain saturation, determines whether the system behaves in a topological or non-topological manner once lasing begins.

Implications for topological photonics

This work has several important consequences. First, it challenges a widely held assumption in topological laser design: that lasing will faithfully inherit the spatial structure of the linear topological mode. The study shows that this assumption can fail, even in clean systems without disorder.

Second, it highlights a subtle breakdown of bulk–boundary correspondence in nonlinear, non-Hermitian systems. In traditional topological physics, bulk properties determine the existence of edge states. Here, nonlinear dynamics can override that connection at the level of the lasing mode.

Third, the findings suggest that designing robust topological lasers requires more than just engineering the passive lattice. Nonlinear effects must be treated as central players, not minor corrections.

Broader relevance beyond lasers

While the study focuses on photonic SSH arrays, its implications extend further. Many quantum systems feature intrinsic nonlinear losses or interactions. The interplay between topology, non-Hermiticity, and nonlinearity is becoming a major theme across physics, from cold atoms to exciton-polariton condensates.

The results also speak to ongoing debates about how topology should be defined and measured in driven, dissipative systems. In such settings, steady-state behavior can differ sharply from predictions based solely on linear eigenmodes.

A closer look at SSH lattices and zero modes

SSH lattices are a foundational model in topological physics. They consist of a chain of sites with alternating strong and weak couplings. When arranged in a certain pattern, the system hosts a zero-energy mode localized at its boundary. This mode is protected by symmetry and topology in the linear regime.

In photonics, SSH lattices have been implemented using waveguide arrays, resonator chains, and laser cavities. Their simplicity makes them ideal for exploring how topology interacts with gain, loss, and nonlinearity.

The new study shows that while SSH topology still exists in the background, lasing dynamics can effectively mask or reshape its observable consequences.

Why this study stands out

Unlike many earlier works, this research does not rely on disorder, imperfections, or competing modes to explain the loss of localization. Instead, it demonstrates that nonlinear gain saturation alone is enough to drive a qualitative change in behavior.

By focusing on regimes where the zero mode is stable, the authors make a strong case that these effects are not just theoretical curiosities, but realistic features of operational laser systems.

Final thoughts

Topological photonics remains a powerful and promising field, but this study serves as a reminder that real-world physics is rarely as clean as our idealized models. Zero lasing modes can exist without being topological, and understanding when and why this happens is essential for both fundamental science and practical device design.

As researchers continue to explore non-Hermitian and nonlinear systems, results like these will play a crucial role in shaping the next generation of photonic technologies.

Research paper: https://www.nature.com/articles/s42005-025-02377-7